Lagrange's mean value theorem in Python
Lagrange's mean value theorem in Python:-
If we talk about Rolle’s Theorem - it is a specific case of the mean value of theorem which satisfies certain conditions. But in the case of Lagrange’s mean value theorem is the mean value theorem itself or also called first mean value theorem. Here in this section, we will about Lagrange’s mean value theorems. By mean we understand the average of the given values. But in the case of integrals, the process of finding the mean value of two different functions is different. Let us learn the mean value of such functions along with their geometrical interpretation.
In the case of Lagrange’s Mean Value Theorem If a function f is described on the closed interval [a,b] satisfying the following conditions –
i) The function f is said to be continuous on the closed interval [a, b]
ii)The function f is said to be differentiable on the open interval (a, b)
Then there exists a value x = c in such a way that
f'(c) = [f(b) – f(a)]/(b-a)
This theorem is also called as the first mean value theorem or Lagrange’s mean value theorem
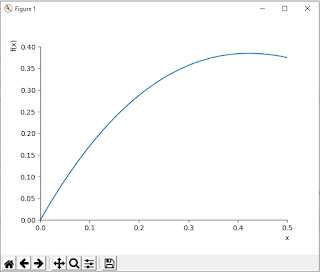
1.IIIustrate the geometric meaning of Lagrange's mean value theorem of the following function on the given interval:
f(x) = x(x-1)(x-2) at x = (0,1/2)
from mpmath import *
from sympy import *
import random
import cmath
x,y,z,a,b,c = symbols('x y z a b c')
init_printing(use_unicode=True)
flagcontinuity = Falseflagdifferentiability = Falsedef h(x):
expr = x*(x-1)*(x-2)
return expr
print(h(x))
print('generating graph of equation')
plot(h(x),(x,0,1/2))
Output:
x*(x - 2)*(x - 1)generating graph of equation
 |
| Lagrange's mean value theorem in Python |
print('checking first condition of theorem')
lnhdlimit_pos = limit(h(x),x,0,'+')
lnhdlimit_neg = limit(h(x),x,0,'-')
print(lnhdlimit_pos)
print(lnhdlimit_neg)
rnhdlimit_pos = limit(h(x),x,1/2,'+')
rnhdlimit_neg = limit(h(x),x,1/2,'-')
print(rnhdlimit_pos)
print(rnhdlimit_neg)
if(lnhdlimit_pos==lnhdlimit_neg)and(lnhdlimit_neg==h(0))and(rnhdlimit_pos==rnhdlimit_neg)and(rnhdlimit_neg==h(1/2)):
print('function `is continous')
else:
print('function is discontinous')
flagcontinuity= True

First condition of Lagrange's mean value theorem in Python
print('checking the second condition of the theorem')
for i in range(0,1):
j = random.uniform(0,0.5)
difflnhd = diff(limit(h(x),x,j,'+'))
diffrnhd = diff(limit(h(x),x,j,'-'))
print(difflnhd)
print(diffrnhd)
if(difflnhd==diffrnhd):
print('function is differentiable')
else:
print('function is not differentiable')
flagdifferentiability = True
 |
| Second Condition of Lagrange's mean value theorem |
if(flagcontinuity==True)or(flagdifferentiability==True): print('lagrange theorem is not applicable') else: print('lagrange theorem is applicable') print('finding the derivative of the given function') d = diff(h(x),x) print('derivative of h(x) is',d) print('so there exit some contant c') print('enter the value of a,b') a = float(input('enter value of a')) b = float(input('enter value of b')) ratio = (h(b)-h(a))/(b-a) print(ratio) rd = round(ratio,2) print('round value of ration at two decimal points',rd) print('let find the value of c') print(diff(h(c),c),'=',rd) z = diff(h(c),c) simplify(diff(h(c),c)) print(solve((c*(c-2)+c*(c-1)+(c-2)*(c-1)-rd),c)) ar = solve((c*(c-2)+c*(c-1)+(c-2)*(c-1)-rd),c) print('value of c is',ar) print('it lies between a and b',a,b) plot(h(x),(x,0,1/2),ar[0],ar[1])
 |
 |
Lagrange's mean value theorem in PythonSummary: In this section, we discuss the Lagrange's mean value theorem, conditions of the Lagrange's mean value theorem. In this first, we import all libraries that are necessary for the implementation of Lagrange's mean value theorem. You may also check the Python Libraries tutorial if you want to know how to import these libraries. Sympy stands for Symbolic Python so in this case we from sympy import *. This means it includes all the module all in Sympy. then we impost cmath library which is necessary when we implement mathematical equations. We used lnhdlimit_pos (left neighborhood limit) and rnhdlimit_pos (right neighborhood limit) for both positive and negative. Then we check all the conditions of Lagrange's mean value theorem one by one using Python Code. If all the conditions satisfied are then checked if the langrange theorem is applicable or not applicable. If the theorem is applicable then find the derivative of the given function, print the derivative of the equation and plot the graph of the given equation.




.png)
.png)