Find the limit of a function as x tends to Zero
Find the limit of a function as x tends to Zero
In this unit, we explain what it means when the Limit of a function tends to Zero. To master the techniques described here, it is important that you do many exercises to make it second nature. In this example, we use Python programming to check the limit when x goes to Zero. In mathematics, a limit is a value that a function as the input "approach" some value.
Limits are integral to calculus (and mathematical evaluation in general) and are used to define continuity, derivatives, and integrals. In this article, various python libraries are used. Check this if you want to compute the limit of a function in Python without plotting using Sympy. Now Let's take a look at how to find the limit for the given function when x tends to Zero in Python code.
The limit of a function
In the case of Mathematics, The limit of a function is a fundamental concept in calculus. It analysis concerning the behavior of that function near a particular input.Formal definitions, first formulated in the 19th century, are given below. Informally, a function f assigns an output f (x) to each input x. We say that the limit on the input L of the function is L: this means that f (x) moves closer to L and closer to x because x moves closer to P and moves. More specifically, when F is applied sufficiently close to P for any input, the output value is arbitrarily forced to be close to L.
On the other hand, if the input is moved too close to P for outputs that remain at a certain distance, then we say the limit does not exist.
The limit of a function has many applications in modern calculus. In particular, several definitions of continuity employ the limit: broadly, a function is continuous if all of its boundaries agree with the values of the function. It also appears in the definition of the derivative: in the algorithm of a variable, it is the finite value of the slope of the second lines in the graph of a function. has many applications in modern calculus. In particular, several definitions of continuity employ the limit: broadly, a function is continuous if all of its boundaries agree with the values of the function. It also appears in the definition of the derivative: in the algorithm of a variable, it is the finite value of the slope of the second lines in the graph of a function.
Let's take a look at Python code on how to plot the limit of a function as x tends to zero.
1. Discuss the Limit of the following function as x tends to zero.

import numpy as np
from sympy import *
x = symbols('x')
init_printing(use_unicode=True)
print(limit(1/x,x,0,'+'))
print(limit(1/x,x,0,'-'))
plot(1/x)
Output: oo -oo

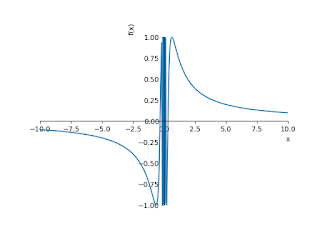
2. Discuss the Limit of the following function as x tends to zero.import numpy as np from sympy import * x = symbols('x') init_printing(use_unicode=True) print(limit(sin(1/x),x,0,'+')) print(limit(sin(1/x),x,0,'-')) plot(sin(1/x))Output: AccumBounds(-1, 1) AccumBounds(-1, 1)3. Discuss the Limit of the following function as x tends to zero.

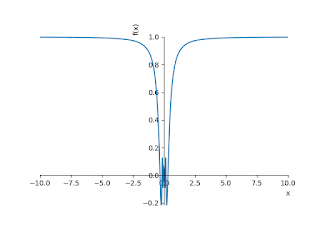
import numpy as np from sympy import * x = symbols('x') init_printing(use_unicode=True) print(limit(cos(1/x),x,0,'+')) print(limit(cos(1/x),x,0,'-')) plot(cos(1/x))Output: AccumBounds(-1, 1) AccumBounds(-1, 1)import numpy as np from sympy import * x = symbols('x') init_printing(use_unicode=True) print(limit(x*cos(1/x),x,0,'+')) print(limit(x*cos(1/x),x,0,'-')) plot(x*cos(1/x))Output:06. Discuss the Limit of the following function as x tends to zero.import numpy as np from sympy import * x = symbols('x') init_printing(use_unicode=True) print(limit(x**2*sin(1/x),x,0,'+')) print(limit(x**2*sin(1/x),x,0,'-')) plot(x**2*sin(1/x))Output: 07. Discuss the Limit of the following function as x tends to zero.import numpy as np from sympy import * x = symbols('x') init_printing(use_unicode=True) print(limit(x**2*cos(1/x),x,0,'+')) print(limit(x**2*cos(1/x),x,0,'-')) plot(x**2*cos(1/x))Output: 0













.png)