How to compute limit in Python using Sympy
How to compute limit in Python using Sympy
This section covers how to perform basic calculus functions such as derivatives, integrals, limits, and series expansions in SymPy. In this section, we cover how to compute limit in Python using Sympy. Sympy is a Symbolic Python that is used to compute Limit and other basic functions. But in this, we focus on how to compute limit in Python using Sympy in an easy way and also discuss the Sympy library. What is Sympy how it can be used in Symbols. You may also check Python libraries if you want to know how to install and import Sympy. If you already know then you can skip this.
Calculate Limits
Limits are easy to use in SymPy. They follow the syntax limit (function, variable, point), so to calculate the limit of f (x) as x -> 0, you will issue the limit (f, x, 0).
Limit in Mathematics
In mathematics, a limit is a value that approaches ("index") some input "(or index)" as a function (or sequence) "approaches". Calculus (and mathematical analysis in general) requires limit and is used to define continuity, derivatization, and integrals.The concept of the limit of a sequence is generalized to the concept of the limit of a topological net and is closely related to the limit and direct boundary in the category theory.
What is SymPy?
SymPy is a Python library for symbolic mathematics. Its purpose is to be fully featuredComputer algebra system that can compete directly with commercial alternatives (mathematician, maple)
While keeping the code as simple as possible to be simple and easily extensible. It is written entirely in Python and does not require any external library.
SymPy defines three numeric types: real, rational, and integer. Rational square is an integer representing a rational number in the form of two pairs:
numerator and denominator.
therefore, represents rational (1,2) 1/2, rational (5,2) 5/2.
SymPy uses mpmath in the background, which makes it possible to perform calculations using arbitrary arithmetic. In this way, some special constants, such as E, P, OO (Infinity), are considered as symbols and Can be evaluated with arbitrary precision.
Sympy - Symbols
Unlike other computer algebra systems, in SymPy you have to declare symbolic variables.
from sympy import *
x = symbol ('x')
y = symbol ('y')
Now take a look at how to compute limit in Python using Sympy. The limit can be carried out by sp.limit(f,x,0).
1. Compute the limit of sin(x)/x using Sympy.
from sympy import *
x = symbols('x')
f = sin(x)/x
y = limit(f,x,0)
print(y)
Output: 12. Compute the limit of 1/x using Sympy.from sympy import * x = symbols('x') f = 1/x y = limit(f,x,0) print(y)Output: oo3. Compute the limit of the given function using Sympy.
Output: 04. Compute the limit of the given function using Sympy.
from sympy import * x = symbols('x') f = exp(-x) y = limit(f,x,0) print(y) Output: 15. Compute the limit of 1/x**2 using Sympy.from sympy import * x = symbols('x') f = 1/x**2y = limit(f,x,0) print(y) Output: oofrom sympy import * x = symbols('x') f = exp(x) y = limit(f,x,0) print(y)Output: 1
from sympy import * x = symbols('x') f = log(x) y = limit(f,x,0) print(y) Output: -oo
from sympy import * x = symbols('x') f = ((4*(x**3)-2*x-6)/(-x**3+x**2+1)) y = limit(f,x,0) print(y) Output: -6






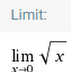


.png)
.png)