Solving First-order Ordinary differential equations
Solving First-order Ordinary differential equations
In this section, We discuss Ordinary Differential equations the method to solving first order Ordinary differential equations in Python Programming. The first thing we learn here is What Differential equations, a form of the differential equations. Then we moved further to solve the ODE order first and plot these equations in Python.
In this, we used from scipy.integrate import odeint to solving first-order Ordinary differential equations. The differential equations are solved using scipy.integrate package using the function ODEINT in Python Programming. If we talk more about also need numpy and matplotlib library. Check this article to know more about these libraries
So let's start with Differential equations also discuss which form is used to write the differential equations.
Differential equations
Differential equations are called partial differential equations (PDE) or Ordinary differential equations (ODE), whether they are included or not partial derivatives. A solution (or special solution) of the differential equation of order n defines a function and has different times on one Domain D has the property that holds the functional equation obtained by substituting the function and its n derivatives into the differential equation D.The differential equations in the form,
Equation 1.

A first-order differential equation is an equation in which ƒ(x, y) is a function of two variables defined on a region in the XY-plane. The equation is of the first order because it contains only the first derivative dy/dx.
y' = f(x,y) and

all these are equivalent to equation 1.
1. Solving Ordinary differential equation of order first using Eq.

from scipy.integrate import odeint
import numpy as np
from matplotlib import pyplot as plt
def f(y,x):
return x
y0 = 1xs = np.arange(0,1,0.1)
ys = odeint(f,y0,xs)
plt.plot(xs,ys,'-')
plt.plot(xs,ys,'ro')
plt.xlabel('x values')
plt.ylabel('y values')
plt.title('Differential equation: dy/dx=x, y(0)=1, xrange=[0,1]')
plt.show()
Output:

2. Solving Ordinary differential equation of order first using Eq.

from scipy.integrate import odeint
import numpy as np
from matplotlib import pyplot as plt
def f(y,x):
return y/x
y1 = 1xs = np.arange(1,10,1)
ys = odeint(f,y1,xs)
plt.plot(xs,ys,'-')
plt.plot(xs,ys,'ro')
plt.xlabel('x values')
plt.ylabel('y values')
plt.title('Differential equation: dy/dx=y/x, y(1)=1')
plt.show()

3. Solving Ordinary differential equation of order first using Eq.

from scipy.integrate import odeint
import numpy as np
from matplotlib import pyplot as plt
def f(y,x):
return (x*y/(np.sqrt(y**2+x)))
y0 = 1xs = np.arange(0,5,0.25)
ys = odeint(f,y0,xs)
plt.plot(xs,ys,'-')
plt.plot(xs,ys,'ro')
plt.xlabel('x values')
plt.ylabel('y values')
plt.title('Differential equation: dy/dx=(x*y/(np.sqrt(y**2+x))')
plt.show()

4. Solving Ordinary differential equation of order first using Eq.

from scipy.integrate import odeint import numpy as np from matplotlib import pyplot as plt def f(y,x): return (x +y) y0 = 0xs = np.arange(0,2,0.1) ys = odeint(f,y0,xs) plt.plot(xs,ys,'-') plt.plot(xs,ys,'ro') plt.xlabel('x values') plt.ylabel('y values') plt.title('Differential equation: dy/dx=x+y') plt.show()

5. Solving Ordinary differential equation of order first using Eq.from scipy.integrate import odeint import numpy as np from matplotlib import pyplot as plt def f(y,x): return (3*y-x) y0 = 0xs = np.arange(0,3,0.1) ys = odeint(f,y0,xs) plt.plot(xs,ys,'-') plt.plot(xs,ys,'ro') plt.xlabel('x values') plt.ylabel('y values') plt.title('Differential equation: dy/dx=(3*y-x)') plt.show()6. Solving Ordinary differential equation of order first using Eq.from scipy.integrate import odeint import numpy as np from matplotlib import pyplot as plt def f(y,x): return (x**2) y0 = 1xs = np.arange(0,5,0.25) ys = odeint(f,y0,xs) plt.plot(xs,ys,'-') plt.plot(xs,ys,'ro') plt.xlabel('x values') plt.ylabel('y values') plt.title('Differential equation: dy/dx=(x**2)') plt.show()





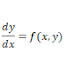


.png)
.png)