Graph of Parabola, Hyperbola and Ellipse function?
Graph of Parabola, Hyperbola and Ellipse function?
In this section, we discuss how to plot the graph of Parabola, Hyperbola and Ellipse function in Python programming using matplotlib. All of these we discuss one by one in detail with code in an easy way.
In Python, you can plot the graphs by using the popular library Matplotlib. so first we have to install matplotlib then import matplotlib into the program.
Before moving forward we first read about the Conic sections. What are the Conic sections what are there uses and how it is related to Parabola, Hyperbola, and Ellipse?.
Let's start with Introduction to Conic sections.
There are three types of conic sections are the hyperbola, the parabola, and the ellipse. The circle is a type of ellipse and is from time to time viewed to be a fourth kind of conic section.
Conic sections can be generated by using intersecting a plane with a cone. A cone has two identically shaped components called nappes. One nappe is what most people mean by “cone,” and has the structure of a party hat.
Conic sections are generated by using the intersection of a plane with a cone. If the plane is parallel to the axis of revolution (the y-axis), then the conic part is a hyperbola. If the plane is parallel to the generating line, the conic part is a parabola.
If the plane is perpendicular to the axis of revolution, then the conic section is a circle. If the plane intersects one nappe at an angle to the axis (other than 90 degrees), then the conic part is an ellipse
.
Each type of conic section is described in detail below.
Parabola
A parabola is the set of all points whose distance from a fixed point, known as the focus, is equal to the distance from a fixed line, known as the directrix. The point midway between the focus and the directrix is known as the vertex of the parabola.
Hyperbolas
A hyperbola is the set of all points where the difference between their distances from two fixed points (the foci) is constant. there are two foci and two directrices in a hyperbola, Hyperbolas also have two asymptotes.
Ellipse
In an ellipse, it is a set of all points for which the sum of the distances from two fixed points is constant. In an ellipse, there are two foci and two directrices.
Ellipses are frequent in physics, astronomy, and engineering. For example, the orbit of each planet in the solar system is about an ellipse with the Sun at one focus point (more precisely, the focus is the barycenter of the Sun–planet pair). The same is actual for moons orbiting planets and all other systems of two astronomical bodies.
In Python, you can plot the graphs by using the popular library Matplotlib. so first we have to install matplotlib then import matplotlib into the program.
Before moving forward we first read about the Conic sections. What are the Conic sections what are there uses and how it is related to Parabola, Hyperbola, and Ellipse?.
Let's start with Introduction to Conic sections.
Introduction to Conic Sections:
A conic section (or simply conic) is a curve acquired as the intersection of the surface of a cone with a plane.There are three types of conic sections are the hyperbola, the parabola, and the ellipse. The circle is a type of ellipse and is from time to time viewed to be a fourth kind of conic section.
Conic sections can be generated by using intersecting a plane with a cone. A cone has two identically shaped components called nappes. One nappe is what most people mean by “cone,” and has the structure of a party hat.
Conic sections are generated by using the intersection of a plane with a cone. If the plane is parallel to the axis of revolution (the y-axis), then the conic part is a hyperbola. If the plane is parallel to the generating line, the conic part is a parabola.
If the plane is perpendicular to the axis of revolution, then the conic section is a circle. If the plane intersects one nappe at an angle to the axis (other than 90 degrees), then the conic part is an ellipse
.
Each type of conic section is described in detail below.
Parabola
A parabola is the set of all points whose distance from a fixed point, known as the focus, is equal to the distance from a fixed line, known as the directrix. The point midway between the focus and the directrix is known as the vertex of the parabola.
Hyperbolas
A hyperbola is the set of all points where the difference between their distances from two fixed points (the foci) is constant. there are two foci and two directrices in a hyperbola, Hyperbolas also have two asymptotes.
Ellipse
In an ellipse, it is a set of all points for which the sum of the distances from two fixed points is constant. In an ellipse, there are two foci and two directrices.
Ellipses are frequent in physics, astronomy, and engineering. For example, the orbit of each planet in the solar system is about an ellipse with the Sun at one focus point (more precisely, the focus is the barycenter of the Sun–planet pair). The same is actual for moons orbiting planets and all other systems of two astronomical bodies.
Graph of Parabola:-
Python Code:
import numpy as np
from matplotlib import pyplot as plt
x = np.linspace(-100,100)
a = 1b = 2c = 36y = a*x**2+b*x+c
plt.plot(x,y)
plt.xlabel('x values')
plt.ylabel('y values')
plt.title('graph of parabola')
plt.grid(True)
plt.show()
Output:
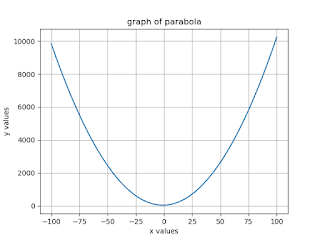
Graph of Hyperbola:-
Python Code:
import numpy as np
from matplotlib import pyplot as plt
x = np.linspace(-100,100)
a = 1b = 2y = np.sqrt((x/a)**2-1*b**2)
plt.plot(x,y)
plt.plot(x,-y)
plt.xlabel('x values')
plt.ylabel('y values')
plt.title('graph of hyperbola')
plt.grid(True)
plt.show()
Output:

Graph of Ellipse:-
Python Code:
import numpy as np
from matplotlib import pyplot as plt
x = np.linspace(-2,2)
a = 2b = 4y = np.sqrt(1-(x/a)**2)*b**2plt.plot(x,y)
plt.plot(x,-y)
plt.xlabel('x values')
plt.ylabel('y values')
plt.title('graph of ellipse')
plt.grid(True)
plt.show()
Output:
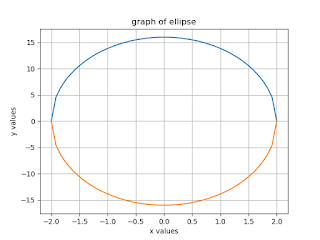




.png)
.png)